20%OFF（割引）だと思って買ったら20%増量だった！どちらがお得？

昨日の夕方スーパーに行ったのですが、割り引きシールだと思って買って、家に帰ってから見たら増量のシールでした。

まあどっちでもいいんですけど、ふとどちらが得なのか考えてみようと思って。

単純にするために元々100g（グラム）で1000円の商品だったとします。（良い肉買ってるなあ～じゃないですyo）

1g単位の金額を計算して比較すればいいのかな。

先ず、20%引きの場合は、1000円が20%割引で800円になります。
100gで800円になるのだから1g当たりは、
800 / 100 = 8 –> 1g当たり8円です。

次に、20%増量の場合は、金額は変わらず量が120gとなります。
120gで1000円なのだから、
1000 / 120 = 8.333…. –> 1g当たり約8.33円です。

よって20%引きの方が安くなるという結果になりました。

式で表すと、
割引・増量率（%）をxとすると、
割引1g当たり金額 = 元の金額（1-x/100）/ グラム数
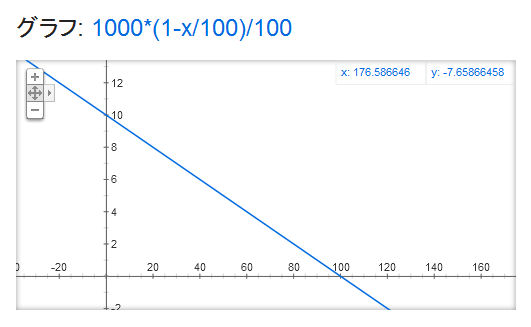
増量1g当たり金額 = 元の金額 / （グラム数（1+x/100））

グラフにするとこんな感じかな。
増量の場合は分母にxが来るのでy=1/xの様に曲線になります。

＜割引グラフ＞

＜増量グラフ＞

＜スケールを同じにして重ね合わせる＞

結果：同じ割合の割引と増量なら、割引の方がお得。100%で考えれば割引は0円で増量は半額になるのだから、感覚的には計算するまでも無く当然か。（本当は増量グラフが割引グラフの下に来ないことを証明しないといけないのですよね。接線だとすればいいのかな）

⊿

しかし、ここでクレカで払って、支払金額に1%のポイントが付与される場合を考えてみましょう。

800円なら1%の8円戻ってくるのだから実質800-8=792円で購入していることになります。
1000円なら1%の10円戻ってくるのだから実質1000-10=990円で購入していることになります。

割引時：792円 / 100g = 7.92 円/g –> 1g当たり7.92円です。
増量時：990円 / 120g = 8.25 円/g –> 1g当たり8.25円です。

よってポイントが付与される場合も、20%引きの方が安くなるという結果になりました。100%のポイントが付くならどちらも割引・増量率に関わらず実質無料ということですからね。グラフで言うと両方とも還元ポイントが100%に近づくにつれてx軸に近づいていくイメージかな。それ以上の還元率は買う方が儲かってしまうので考えなくてもいいでしょう。

式で表してみます。

割引・増量率（%）をxとすると、
割引1g当たり金額 = 元の金額（1-x/100）/ グラム数
増量1g当たり金額 = 元の金額 / （グラム数（1+x/100））

先程考えたこれに、分子を「値段」–>「ポイント還元後の値段」とすればいいということかな。

ポイント還元率(%)をpとすると、
割引の場合は割り引いた金額から更に還元されたポイント分を引けば値段になるので、
「元の金額（1-x/100）」が割引後の値段だから、これからポイント分を引くと
還元後の値段 –> 元の金額（1-x/100）- 元の金額（1-x/100）（p/100）
還元後の値段 –> 元の金額（1-x/100）（1-p/100）

増量の場合は、還元されたポイント分だけを引けば値段になるので、
還元後の値段 –> 元の金額 – 元の金額（p/100）
還元後の値段 –> 元の金額（1-p/100）

よって、割引・増量率（%）をx、ポイント還元率(%)をpとすると、
割引1g当たり金額 = 元の金額（1-x/100）（1-p/100）/ グラム数
増量1g当たり金額 = 元の金額（1-p/100） / （グラム数（1+x/100））

pを0-100で変えていくと上の様なグラフが作れるはずです。p=0の場合がポイント還元を考慮しない場合と同じです。（1-x/100）の部分が20%割引の0.8とか、（1-p/100）が1%還元（割引と同じ）の0.99と考えると分かりやすいかな。（式にしようとすると逆に解りにくい…）

結論：ポイントが付いても、同じ割合の割引と増量なら、割引の方がお得。

ていう考え方でいいのかしら。というか常識だったのかも。買い物に交通費がかかるから増量の方がスーパーへ行く回数が少なくて安くなるとかいうのは知らんよ。

気に入ったら応援していただけると嬉しいです (^^)/